Python으로 블랙리터만 (Black-Litterman) 모델 구현하기

작성일 Edited on Disqus:

0. Introduction

금융 데이터를 이런저런 방식으로 분석해서 결과를 팀원들에게 공유하면, 반드시 나오는 중요한 질문이 하나 있습니다. 해당 결과를 어떻게 전략화 할 수 있냐는 겁니다. 분석 그 자체로써 의미있는 경우도 있지만, 결과적으로 (모델이 되었든 매니저가 되었든) 누군가는 포트폴리오 구성 및 운용 방식, 즉, 어떤 자산($X$)을 언제($t$), 얼마만큼($w$) 가지고 있어야 하는지에 대한 판단을 내려야 합니다.

포트폴리오 구성과 관련된 모델 중 가장 잘 알려진 이론은 Mean-Variance Optimization Portfolio일 것입니다. 해당 모델의 로직은 논리적이고 직관적이지만, 몇 가지 문제점들이 있습니다.

  1. 입력 데이터의 작은 변화에도 도출되는 포트폴리오 구성비중이 크게 변합니다.
  2. 몇 개의 자산에 비중이 쏠리는 코너 솔루션이 나타나는 경우가 있습니다.
  3. 투자자가 가지고 있는 정보를 녹여낼 수 있는 방법 없습니다. 따라서, 시장에 대한 견해가 다른 매니저일지라도 (같은 hyperparameter를 가지고 있는 경우) 같은 MVO 포트폴리오를 얻게 됩니다.

위 문제점들은 실제 운용을 할 때 걸림돌이 됩니다. (ex. 높은 turnover ratio, 규제위반, 모델에 들어가지 않은 추가적인 정보 반영 불가 등) 이러한 문제점들을 해결하기 위해, 골드만삭스의 Fischer Black과 Robert Litterman이 1990년에 개발하고 1992년에 발표한 포트폴리오 최적화 방법론이 Black-Litterman Model입니다.

본 포스팅은 Black-Litterman Portfolio Model의 전체적인 프로세스를 이해하고, Python으로 이를 구현해보는 과정을 정리해 놓은 글입니다. 내용에 문제나 개선점이 있는 경우, 피드백을 주시면 감사하겠습니다! 😀

0. References

  • Idzorek, T. “A step-by-step guide to the Black-Litterman model: Incorporating user-specified confidence levels.”, 2007
    • 모델을 이해하는데 가장 많이 참조한 자료로, 포스팅의 notation들은 해당 자료를 따라갔습니다.
  • Stuart, J. “Black-Litterman Portfolio Allocation Model in Python“, 2020
    • Reverse Optimization Process를 이해하는데 큰 도움이 된 포스팅입니다.
  • Tim Wilding. “Struggling with tau in Black-Litterman“, 2018
  • Walters, Jay. “The Factor Tau in the Black-Litterman Model”, 2010
    • $\tau$ 값을 이해하는데 도움이 됐었던 포스팅과 자료입니다.
  • Satchell, S. and Scowcroft, A. “A Demystification of the Black-Litterman model: Managing Quantitative and Traditional Construction.”, 2000
  • Blamont, D. and Firoozy, N. “Asset Allocation Model.”, 2003
  • Olsson, Sebastian & Trollsten, Viktor. “The Black-Litterman Asset Allocation Model”, 2018

1. Top-down

모델을 자세히 살펴보기에 앞서서, 모델에 사용되는 수식을 살펴보면 다음과 같습니다.

\begin{align} E[R] &= [(\tau\Sigma)^{-1}+P^T\Omega^{-1}P]^{-1}[(\tau\Sigma)^{-1}\Pi+P^T\Omega^{-1}Q] \\ \hat{w} &= (\Sigma^{-1}E[R])/(1^T\Sigma^{-1}E[R]) \end{align} \begin{align*} N &\qquad\text{is the number of assets} \\ K &\qquad\text{is the number of views} \\ E[R] &\qquad\text{is the new (posterior) Combined Return Vector (N x 1 column vector)} \\ \tau &\qquad\text{is a scalar} \\ \Sigma &\qquad\text{is the covariance matrix of excess returns (N x N matrix)} \\ P &\qquad\text{is a matrix that identifies the assets involved in the views} \\ &\qquad\text{(K x N matrix or 1 x N row vector in the special case of 1 view)} \\ \Omega &\qquad\text{is a diagonal covariance matrix of error terms from the expressed views} \\ &\qquad\text{representing the uncertainty in each view (K x K matrix)} \\ \Pi &\qquad\text{is the Implied Equilibrium Return Vector (N x 1 column vector)} \\ Q &\qquad\text{is the View Vector (K x 1 column vector)} \\ \hat{w} &\qquad\text{is the new portfolio weight (N x 1 column vector) derived by the model} \\ \lambda &\qquad\text{is the risk aversion coefficient} \end{align*}

수식이 엄청 복잡해 보이지만, 간단하게 요약하자면 수식(1)은 시장 데이터를 통해 도출된 “적당한” 수익률($\Pi$)과 투자자의 전망($Q$)을 “잘” 조합하여 새로운 기대수익률($E[R]$)을 만드는 과정입니다. 이렇게 도출된 기대수익률을 수식(2, unconstrained mean-variance maximization)와 같이 사용하여 새로운 포트폴리오 비중($\hat{w}$)을 구하는 것이, 모델의 최종 목표입니다.

이제 각각의 input들이 어떤 의미를 가지고 어떻게 설정해야 하는지, 소스코드가 진행되는 순서를 따라 예시와 함께 살펴봅시다.

2. Bottom-up (with an example)

2.1. $N$ : The Number of Assets

모델에 사용되는 자산의 개수입니다.

이번 포스팅에서는, 국내 주식 10개 섹터 수익률 데이터를 사용하기로 합니다. 섹터별 수익률 데이터(monthly_excess_returns)와 각 섹터별 비중(w_mkt) 데이터가 필요합니다.

>>> import numpy as np
>>> import pandas as pd
>>> from numpy.linalg import inv

>>> monthly_excess_returns
일자          에너지      소재    산업재  ...        IT  통신서비스  유틸리티
2000-02-29  0.064542 -0.101358 -0.084858  ...  0.079742   -0.044158 -0.160058
2000-03-31  0.169433  0.027033  0.054333  ...  0.044533   -0.091467  0.103133
2000-04-30 -0.190800 -0.175200 -0.187300  ... -0.247900   -0.275900  0.035600
2000-05-31 -0.072333 -0.098433 -0.122233  ... -0.050033    0.138067 -0.072133
2000-06-30  0.112958  0.061258  0.065258  ...  0.143958    0.045258  0.124458
              ...       ...       ...  ...       ...         ...       ...
2020-08-31  0.043058  0.144558  0.016958  ... -0.024642    0.083358  0.040158
2020-09-30 -0.072250 -0.049650 -0.002950  ...  0.018750   -0.025350 -0.001750
2020-10-31 -0.036650 -0.001250 -0.004250  ... -0.041450   -0.077950 -0.000150
2020-11-30  0.224950  0.186950  0.125250  ...  0.147450    0.104550  0.067050
2020-12-29  0.034150  0.036150  0.031150  ...  0.117950   -0.002550  0.149450
[251 rows x 10 columns]

>>> monthly_excess_returns.columns
Index(['에너지', '소재', '산업재', '경기소비재', '필수소비재',
       '의료', '금융', 'IT', '통신서비스', '유틸리티'],
      dtype='object')

>>> w_mkt
에너지        0.0338
소재          0.0912
산업재        0.0924
경기소비재    0.1315
필수소비재    0.0452
의료          0.1120
금융          0.0609
IT            0.4103
통신서비스    0.0134
유틸리티      0.0094
Name: weights, dtype: float64

>>> N = monthly_excess_returns.columns.size
>>> N
10

2.2. $\Sigma$ : Covariance Matrix of Asset Excess Returns

각 자산별 초과수익률의 공분산행렬입니다.

>>> Sigma = monthly_excess_returns.cov()
>>> Sigma
            에너지    소재      산업재    ...  IT        통신서비스  유틸리티
에너지      0.008452  0.004698  0.005392  ...  0.003733  0.002320    0.002559
소재        0.004698  0.005819  0.005411  ...  0.003941  0.002314    0.002564
산업재      0.005392  0.005411  0.007203  ...  0.004600  0.002450    0.002828
경기소비재  0.003492  0.004154  0.004939  ...  0.004753  0.002500    0.002234
필수소비재  0.002434  0.002301  0.002803  ...  0.001972  0.001537    0.001942
의료        0.003892  0.003948  0.004827  ...  0.004101  0.002414    0.001920
금융        0.004257  0.004220  0.004727  ...  0.004055  0.002356    0.002712
IT          0.003733  0.003941  0.004600  ...  0.007571  0.002820    0.001931
통신서비스  0.002320  0.002314  0.002450  ...  0.002820  0.004575    0.002056
유틸리티    0.002559  0.002564  0.002828  ...  0.001931  0.002056    0.004902

2.3. Reverse Optimization Process

Mean-variance optimization process를 추상적으로 요약하자면, 자산의 수익률과 공분산 데이터를 사용하여 “최대 수익률, 최저 변동성”을 가지는 포트폴리오 비중을 구하는 과정이라고 할 수 있습니다. ($f: (\mu, \Sigma) \rightarrow w$) 이를 수식으로 표현한 것이 quadratic risk utility function이고, 최적화 문제를 아래와 같이 나타낼 수 있습니다.

\begin{align} & \underset{w}{\operatorname{max}}\left(w^T\mu - \frac{1}{2}\lambda w^T\Sigma w\right) \\ & \rightarrow \mu - \lambda\Sigma w = 0 \\ & \rightarrow w = (\lambda\Sigma)^{-1}\mu \end{align}

현재 시장에서 관찰할 수 있는 시가총액비중(market capitalization weight)이 위의 최적화 과정에서 도출 된 이상적인 비중이라고 가정 해봅시다. 자산 간 공분산행렬이 있는 경우, 식 (5)를 아래와 같이 변형하여, 각 자산의 “implied returns”를 역으로 구할 수 있습니다. ($g:(w_{mkt}, \Sigma) \rightarrow \mu_{implied}$).

\begin{align} \mu_{implied} = \lambda \Sigma w_{mkt} \end{align}

위와 같이, 시장에서 관측되는 자산비중을 기반으로 균형 수익률을 찾아내는 과정을 “Reverse Optimization Process”이라 하고, 이렇게 구해진 $\mu_{implied}$를 $\Pi$로 표기합니다.

2.4. $\lambda$ : Risk Aversion Coefficient

Reverse optimization process에서, 투자자가 낮은 변동성을 위하여 trade-off 할 수 있는 수익률 수준을 나타내는 상수로써, 일종의 scaling factor 역할을 합니다. 즉, $\lambda$가 클수록, implied returns ($\Pi$) 값이 커지게 됩니다. 값을 설정하는 방법은 자료에 따라 상이하지만, 얼추 다음과 같이 정리할 수 있습니다.

  • 방법 1 : 2.15 ~ 2.65 사이의 값 (BLM 관련 연구자료들의 추천 결과 값)
  • 방법 2 : $\frac{E(R_m)-R_f}{\sigma^2_m}$ (시가총액가중 포트폴리오의 평균 초과수익률 / 분산)

본 포스팅에서는 두 번째 방법을 사용하도록 하겠습니다.

>>> expected_portfolio_excess_return = monthly_excess_returns.mean().multiply(w_mkt).sum()
>>> portfolio_variance = w_mkt.dot(Sigma).dot(w_mkt)
>>> lambd = expected_portfolio_excess_return / portfolio_variance
>>> lambd
1.4956952957871978

2.5. $\Pi$ : Implied Excess Equilibrium Return Vector

위에서 계산한 $\lambda$, $\Sigma$, $w_{mkt}$를 사용하여, 현 시장에서 관측되는 시가총액비중 기반 equilibrium return vector를 다음과 같이 계산합니다.

\begin{equation} \Pi = \lambda \Sigma w_{mkt} \end{equation} \begin{align*} \lambda &\qquad\text{is the risk aversion coefficient} \\ \Sigma &\qquad\text{is the covariance matrix of excess returns (N x N matrix)} \\ w_{mkt} &\qquad\text{is the market capitalization weight (N x 1 column vector) of the assets} \end{align*} 
>>> Pi = lambd * Sigma.dot(w_mkt)
>>> Pi
에너지        0.006078
소재          0.006298
산업재        0.007318
경기소비재    0.006756
필수소비재    0.003517
의료          0.006820
금융          0.006116
IT            0.008216
통신서비스    0.003837
유틸리티      0.003304
dtype: float64

2.6. $K$ : The Number of Views

Black-Litterman Model에서는 투자자가 가지고 있는 정보를 “View”라고 정의합니다. (한글로 해석하면 ‘전망’ 정도 될 것 같습니다.)

이번 예시에서는, 투자자에게 다음과 같은 세 가지의 view가 있다고 가정해봅시다.

  • View 1 : IT 섹터의 초과 수익률이 2%가 될 것이다. (Confidence level = 75%)
  • View 2 : 통신서비스 섹터의 수익률이 유틸리티 섹터의 수익률보다 3% 높을 것이다. (Confidence level = 25%)
  • View 3 : 에너지 섹터의 수익률이 경기소비재, 필수소비재 섹터 수익률보다 1% 높을 것이다. (Confidence level = 50%)

여기서 view 1은 “absolute view”, view 2~3은 “relative view”라고 합니다. Relative view는 outperforming 하는 자산(통신서비스, 에너지)과 underperforming 하는 자산(유틸리티, 경기소비재, 필수소비재)을 포함합니다. 예시의 view 3에서와 같이, outperforming 하는 자산의 수와 underperforming하는 자산의 수가 반드시 동일해야 할 필요는 없습니다.

>>> K = 3

2.7. $Q$ : View Vector

각 view들의 예상 수치(예상 절대/상대수익률)를 포함하는, $K$x$1$ column matrix 입니다. 이번 예시에서의 view vector는 다음과 같습니다.

\begin{equation*} K = \begin{bmatrix} 0.02 \\ 0.03 \\ 0.01 \\ \end{bmatrix} \end{equation*} 
>>> Q = np.array([0.02, 0.03, 0.01])
>>> assert Q.shape == (K,)

2.8. $P$ : Picking Matrix

View에 포함되는 자산들을 명시해주는 행렬입니다. 이번 예시의 경우, 총 3개의 view와 10개의 자산이 있으므로, $P$는 아래와 같은 3x10 행렬이 됩니다.

\begin{equation*} P = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 1 & 0 & 0 & -0.5 & -0.5 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \end{equation*}

첫 번째 행은 첫 번째 view를 나타낸 행으로, 데이터 순서 상 8번 째 자산인 IT섹터를 1로 표시합니다. Absolute view의 경우에는 이와 같이 하나의 column만 1이 되는 row의 형태로 나타납니다.

두 번째와 세 번째 행은, 각각 두 번째와 세 번째 view를 나타냅니다. Outperforming 할 것으로 예상되는 자산은 양수로, underperforming 할 것으로 예상되는 자산은 음수로 표시하여, row의 총 합이 0이 되도록 맞춰줍니다.
View 3와 같이 다수의 자산이 명시가 되어야 하는 경우, outperforming 하는 자산의 합이 1, underperforming 하는 자산의 합이 -1, row의 총 합이 0이 되도록 값을 분배합니다.

위의 행렬 $P$에서 view 3는 underperforming 할 것으로 예상되는 두 자산(경기소비재, 필수소비재)에 대해 동일한 비중으로 값을 설정했습니다. 이 경우, 상대적으로 market cap이 작은 자산의 최종 포트폴리오 비중의 값이 더 많이 변하는 문제가 발생할 수 있습니다. 이러한 문제를 해결하기 위해, $P$ 행렬에서의 비중을 market cap과 동일(혹은 유사)하게 설정하는 방법이 있습니다.

이번 예시에서 경기소비재의 market cap(0.1315)은 필수소비재의 market cap(0.0452)의 약 3배 정도 됩니다. 이를 고려하여 $P$의 값을 아래와 같이 조정할 수 있습니다.

\begin{equation*} P = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 1 & 0 & 0 & -0.75 & -0.25 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \end{equation*}

위에서 정의 된 $P$의 k번째 행(1xN row vector)을 $p_k$로 표기합시다. 이를 사용해서, 각 view를 기반으로 구성된 portfolio의 variance를 $p_k \Sigma p_k^T$로 구할 수 있습니다.

>>> P = np.array([
>>>     [0, 0, 0,    0,    0, 0, 0, 1, 0,  0],
>>>     [0, 0, 0,    0,    0, 0, 0, 0, 1, -1],
>>>     [1, 0, 0, -.75, -.25, 0, 0, 0, 0,  0]
>>> ])
>>> assert P.shape == (K, N)

2.9. $\tau$ : Scalar “Tuning” Constant

Prior estimate of returns($\Pi$)에 대한 불확실 정도를 나타내는 수치입니다. $\tau$ 값이 작을수록, 모델에 의해 계산되는 combined return vector($E[R]$)가 implied equilibrium return($\Pi$)에 가까워지게 됩니다.

아쉽게도, $\tau$ 값을 정하는 명확한 가이드가 없습니다. 아래는 $\tau$값으로 제시된 다양한 후보들입니다.

  • 0.01과 0.05 사이의 값으로 최초 설정한 뒤, tracking error를 줄이는 방향으로 조정
  • 1로 설정 (Satchell and Scowcroft, 2000)
  • *1/(number of observation)*으로 설정 (Blamont and Firoozye, 2003)

좋게 보면 flexible하다고 볼 수 있지만, 일관된 기준이 없다는 점은 모델을 이해하기 어렵고 애매모호하게 만듭니다.

이러한 모호함을 없애기 위하여, 이후 소개드릴 $\Omega$의 값에 $\tau$를 factor-out 시킬 수 있도록 값을 설정하는 방법이 있습니다. (Idzorek, 2007) 이번 포스팅에서는 해당 방법을 사용하겠습니다. 따라서, $\tau$에 0이 아닌 어떠한 값을 넣어도, 최종 결과($E[R]$)에는 영향을 미치지 않게 됩니다.

>>> tau = 1  # 0이 아닌 임의의 값

2.10. $\Omega$ : Uncertainty Matrix of Views

개별 view들의 불확실 정도를 나타내는 대각행렬입니다. 행렬의 원소인 $\omega_k$가 0에 가까울 수록 view k의 confidence가 100%에 가깝다는 것을 의미하고, $\omega_k$가 클수록 해당 view의 불확실성이 높음을 의미합니다.

\begin{equation} \Omega = \begin{bmatrix} \omega_1 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \omega_k \\ \end{bmatrix} \end{equation}

사용자가 개별 view에 대한 confidence 정보를 가지고 있는 경우, $\Omega$의 값을 직접 입력할 수도 있지만, 이번 포스팅에서는 개별 view를 기반으로 생성된 portfolio의 variance를 이용하는 방법을 사용하겠습니다. (Confidence level of views를 기반으로 $\Omega$를 정하는 방법은 본 포스팅의 이후 챕터에서 확인하실 수 있습니다.)

\begin{equation*} \Omega = diag(P(\tau\Sigma)P^T) = \begin{bmatrix} (p_1 \Sigma p_1^T)*\tau & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & (p_K \Sigma p_K^T)*\tau \\ \end{bmatrix} \end{equation*}

위와 같이 $\Omega$를 설정할 경우, $\tau$ 값이 변해도 $E[R]$ 값이 변하지 않습니다. $\tau$와 $\Omega$값이 데이터를 기반으로 계산이 되므로, 매니저는 view와 관련된 input만 신경을 쓰면 됩니다.

>>> Omega = tau*P.dot(Sigma).dot(P.T) * np.eye(K)
>>> Omega
array([[ 0.0075706 ,  0.        , -0.        ],
       [ 0.        ,  0.00536469, -0.        ],
       [-0.        , -0.        ,  0.00634097]])

단, 이번 포스팅에서와 같이 데이터를 기반으로 $\tau$와 $\Omega$를 정하는 방법은 모델을 사용하는 여러가지 방법 중 하나임을 인지할 필요가 있습니다. 필요시, 해당 값들을 변경해가며 최적의 모델 결과를 도출하면 되겠습니다.

3. Run It (but without confidence level of views)

모델에 필요한 데이터들이 준비됐습니다. 이를 기반으로 $E[R]$과 $\hat{w}$를 다음과 같이 구할 수 있습니다.

>>> ER = Pi + tau*Sigma.dot(P.T).dot(inv(P.dot(tau*Sigma).dot(P.T) + Omega).dot(Q - P.dot(Pi)))
... # 수식(1)을 다르게 표현한 수식으로, 동일한 결과값을 계산합니다
>>> ER
에너지       0.012334
소재         0.009002
산업재       0.010075
경기소비재   0.009281
필수소비재   0.003478
의료         0.010962
금융         0.008156
IT           0.015176
통신서비스   0.012539
유틸리티    -0.002864
dtype: float64

>>> w_hat = inv(Sigma).dot(ER)
>>> w_hat = pd.Series(w_hat / w_hat.sum(), index=R.columns)
>>> w_hat
에너지       0.430068
소재         0.063951
산업재       0.064792
경기소비재  -0.212565
필수소비재  -0.069897
의료         0.078536
금융         0.042704
IT           0.586425
통신서비스   1.284972
유틸리티    -1.268985
dtype: float64

>>> w_hat - w_mkt
에너지       0.396268
소재        -0.027249
산업재      -0.027608
경기소비재  -0.344065
필수소비재  -0.115097
의료        -0.033464
금융        -0.018196
IT           0.176125
통신서비스   1.271572
유틸리티    -1.278385
dtype: float64

Outperform 할 것으로 예상되는 섹터들(IT, 통신서비스, 에너지)의 비중은 상향 조정되었고, underperform 할 것으로 예상되는 섹터들(유틸리티, 경기소비재, 필수소비재)의 비중은 하향 조정되었습니다. View에 포함된 자산 뿐만 아니라, 포함되지 않은 자산까지 비중이 전체적으로 조정된 것을 확인할 수 있습니다.

조정된 비중을 살펴보면 설명이 애매한 부분들이 있습니다. 그 중 하나가, 상대적으로 confidence level이 높은 view 1(IT = 2%)에 비해 confidence level이 낮은 view 2(통신서비스 - 유틸리티 = 3%)의 비중이 과도하게 조정이 됐다는 점입니다. 앞선 프로세스를 잘 생각해보면, 아직 각 view의 confidence level을 모델에 반영하지 않았고, 이로 인해 비중의 조정이 $Q$의 값에 지나치게 영향을 많이 받았을 가능성이 있습니다.

4. Considering Confidence Level of Views

본 포스팅에서 사용하는 view들을 다시 한번 확인해봅시다.

  • View 1 : IT 섹터의 초과 수익률이 2%가 될 것이다. (Confidence level = 75%)
  • View 2 : 통신서비스 섹터의 수익률이 유틸리티 섹터의 수익률보다 3% 높을 것이다. (Confidence level = 25%)
  • View 3 : 에너지 섹터의 수익률이 경기소비재, 필수소비재 섹터 수익률보다 1% 높을 것이다. (Confidence level = 50%)

각 view의 confidence level인 75%, 25%, 50%의 값을 모델에 어떻게 녹여낼 수 있을까요? $\Omega$ (uncertainty matrix of views)와 연관이 있는 건 확실해 보이는데, 그렇다고 위의 값($0.75$, $0.25$, $0.50$)을 그대로 행렬에 넣을 수는 없어 보입니다. $\Omega$ 값을 조정해보면서 결과를 살펴봐야 하는데, 이러한 과정을 체계화하여 정리한 하나의 방법을 소개해드리겠습니다. (Idzorek, 2007)

  1. 계산 과정에 필요한 모듈을 import하고 새로 계산될 $\Omega$의 결과를 담아둘 수 있는 행렬을 선언합니다.

    >>> from scipy import optimize
    >>> implied_Omega = np.zeros((K, K))
    >>> k = 0  # 본 포스팅을 line-by-line 실행하는 경우를 위하여 임시로 선언하는 iterator로,
    ...        # 실제 구현에서는 사용되지 않습니다

  2. 각 view의 confidence level들로 이루어진 행렬 $C$를 정의합니다.

    \begin{equation} C = \begin{bmatrix} 0.75 \\ 0.25 \\ 0.50 \\ \end{bmatrix} \end{equation} 
    >>> C = np.array([0.75, 0.25, 0.50])
    >>> assert C.shape == (K,)

이제 각 view를 iterator k를 사용하여 하나씩 iterate하면서 아래의 과정을 진행합니다.

  1. View k가 모델의 유일한 view이고 100% 확실다는 가정하에, $E[R]$ 값과 $w$ 값을 계산합니다. (이 때 계산되는 결과값을 각각 $E[R_{\text{k,100%}}]$ , $w_{\text{k,100%}}$ 라고 표기합니다.)

    View k가 100% 확실한 경우, (1)~(2)의 수식은 아래와 같이 정리할 수 있습니다.

    \begin{align} E[R_{\text{k,100%}}] &= \Pi + \tau\Sigma P_{k}^T (P_k \tau\Sigma P_{k}^T)^{-1}\\ w_{\text{k,100%}} &= (\Sigma^{-1}E[R_{\text{k,100%}}])/(1^T\Sigma^{-1}E[R_{\text{k,100%}}]) \end{align} 
    # 기존 ER을 구하는 수식에서 P를 P[None, k]로, Q를 Q[None, k]로 대체하고,
    # Omega를 생략한 수식입니다.
    >>> ER_k_100 = Pi + tau*Sigma.dot(P[None, k].T).dot(inv(P[None, k].dot(tau * Sigma).dot(P[None, k].T)).dot(Q[None, k] - P[None, k].dot(Pi)))
    >>> w_k_100 = inv(Sigma).dot(ER_k_100)
    >>> w_k_100 = pd.Series(w_k_100 / w_k_100.sum(), index=R.columns)
    >>> w_k_100
    에너지       0.016562
    소재         0.044689
    산업재       0.045277
    경기소비재   0.064436
    필수소비재   0.022148
    의료         0.054881
    금융         0.029842
    IT           0.710993
    통신서비스   0.006566
    유틸리티     0.004606
    dtype: float64

  2. View k가 모델의 유일한 view라는 가정하에, 주어진 confidence level을 반영되었을 경우의 $w$를 추론합니다. (이 때 추론되는 값을 $w_{\text{k,%}}$ 라고 표기합니다.)

    View k의 confidence level이 100%인 경우 포트폴리오 비중이 $w_{\text{k,100%}}$이고, confidence level이 0%인 경우 포트폴리오 비중이 $w_{mkt}$입니다. 따라서, confidence level이 $C_k$인 경우 포트폴리오 비중을 다음과 같이 추론할 수 있습니다.

    \begin{align} w_{\text{k,%}} = w_{mkt} + (w_{\text{k,100%}} - w_{mkt}) * C_k \end{align} 
    >>> w_k_implied = w_mkt + (w_k_100 - w_mkt) * C[k]

  3. View k가 모델의 유일한 view라는 가정하에, view k의 confidence interval $\omega_k$ (omega_k, the k-th diagonal element of $\Omega$) 값을 조절해보면서, confidence interval이 반영된 포트폴리오의 결과가 $w_{\text{k,%}}$에 가깝도록 하는 $\omega_k$ 값을 찾습니다.

    def fun(omega_k):
        # 기존 ER을 구하는 수식에서 P를 P[None, k]로, Q를 Q[None, k]로 대체한 수식입니다.
        ER_k = Pi + tau * Sigma.dot(P[None, k].T).dot(inv(P[None, k].dot(tau * Sigma).dot(P[None, k].T) + omega_k).dot(Q[None, k] - P[None, k].dot(Pi)))
        
        w_k = inv(Sigma).dot(ER_k)
        w_k = pd.Series(w_k / w_k.sum(), index=R.columns)
        
        diff = w_k_implied - w_k
        return diff.T.dot(diff)

    implied_Omega[k][k] = optimize.minimize_scalar(
        fun=fun,
        bounds=(1e-8, 1e+12),
        method='bounded',
    ).x

  4. 위 3~5번 과정을 모든 k에 대해 iterate하여 implied_Omega를 구합니다.

    >>> implied_Omega
    array([[0.00514838, 0.        , 0.        ],
           [0.        , 0.01609381, 0.        ],
           [0.        , 0.        , 0.006342  ]])

이렇게 계산된 implied_Omega 값을 사용하여 전체적인 모델 프로세스를 다시 진행하면, 다음과 같은 결과를 얻을 수 있습니다.

>>> ER_with_CL = Pi + tau * Sigma.dot(P.T).dot(inv(P.dot(tau * Sigma).dot(P.T) + implied_Omega).dot(Q - P.dot(Pi)))
>>> w_hat_with_CL = inv(Sigma).dot(ER_with_CL)
>>> w_hat_with_CL = pd.Series(w_hat_with_CL / w_hat_with_CL.sum(), index=R.columns)
>>> w_hat_with_CL
에너지       0.377316
소재         0.058063
산업재       0.058827
경기소비재  -0.183128
필수소비재  -0.060173
의료         0.071305
금융         0.038772
IT           0.624501
통신서비스   0.583587
유틸리티    -0.569071
dtype: float64

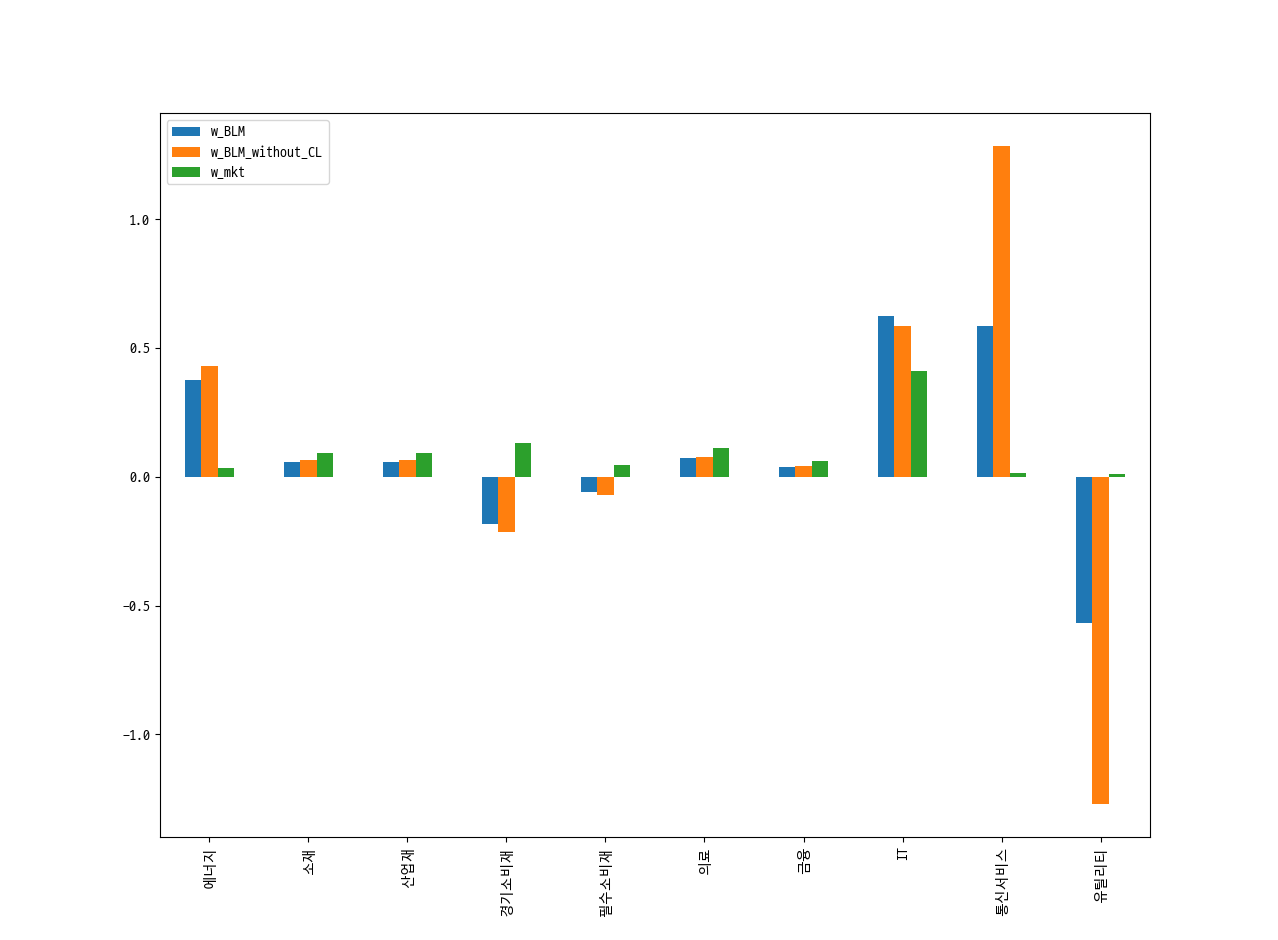
Confidence level이 고려되지 않은 결과보다, 조금 더 설득력 있는 형태의 포트폴리오가 구성되었습니다.

5. Dealing with Constraints

모델의 전체적인 프로세스를 진행하는 과정에서, 포트폴리오의 비중을 구하기 위하여 크게 다음의 두 가지 스텝을 밟았습니다.

  • Black-Litterman 모델을 통해 자산별 기대수익률($E[R]$)을 계산하고,
  • 해당 기대수익률을 기반으로 mean-variance optimization을 적용하여 새로운 비중($\hat{w}$)을 계산했습니다.

본 포스트에서는 제약조건이 없는 mean-variance optimization(unconstrained maximization optimization process)을 가정하였습니다. ($\hat{w} = (\Sigma^{-1}E[R])/(1^T\Sigma^{-1}E[R])$) 만약 포트폴리오 구성 시 제약조건(보유비중, 리스크, 베타, long-only portfolio 등)이 있는 경우, 위의 (2)번 프로세스에 제약조건을 더해 mean-variance optimization을 진행하면 되겠습니다. (이 경우 closed-form solution을 구하는 방법보다는, confidence level을 반영하는 과정에서 scipy.optimize를 사용한 것과 비슷하게 numerical solution을 찾는게 효과적일 것으로 판단됩니다.)